2025-08-21:分割正方形Ⅱ。用go语言,给你一个二维整数数组 squares,其中每个元素 [xi, yi, li] 表示一个与 x 轴平行的正方形:左下角坐标为 (xi, yi)实盘10倍杠杆,边长为 li。请寻找最小的实数 Y,使水平直线 y = Y 将所有正方形的并集划分成上下两部分,且上半部分的面积与下半部分的面积相等。正方形之间可能相互覆盖,重叠区域只计入一次。答案以绝对误差不超过 视为正确。
1
squares[i] = [xi, yi, li]。
squares[i].length == 3。
0
1
所有正方形的总面积不超过 1000000000000000。
输入: squares = [[0,0,1],[2,2,1]]。
输出: 1.00000。
解释:
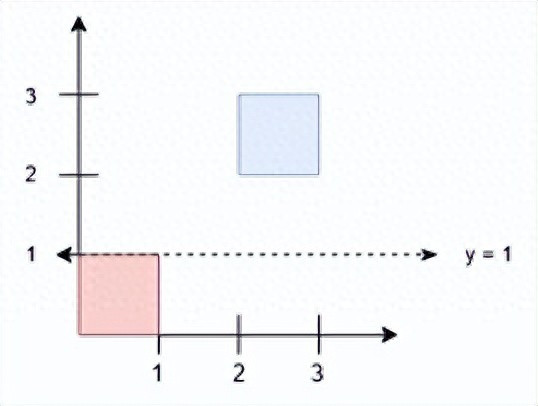
任何在 y = 1 和 y = 2 之间的水平线都会有 1 平方单位的面积在其上方,1 平方单位的面积在其下方。最小的 y 坐标是 1。
题目来自力扣3454。
分步骤描述过程
1. 问题分析:
给定多个与x轴平行的正方形(可能重叠),需要找到一条水平线y=Y,使得所有正方形并集被分成上下两部分,且上下面积相等(总面积的一半)。由于正方形可能重叠,重叠区域只算一次,因此需要计算并集的面积。
2. 离散化横坐标:
• 提取所有正方形的左右边界(即xi和xi+li),排序并去重,得到离散化的横坐标数组xs。这些横坐标将x轴分成多个区间(线段树中的叶子节点),每个区间长度(xs[i+1]-xs[i])作为线段树中该节点维护的底边长度。
3. 事件处理:
• 为每个正方形生成两个事件:下边界(yi)处增加覆盖(delta=1),上边界(yi+li)处减少覆盖(delta=-1)。将所有事件按y坐标排序。
4. 线段树初始化:
• 线段树每个节点维护一段横坐标区间[lx, rx]的信息:
• minCover:该区间内被矩形覆盖的最小次数(实际上这里维护的是当前区间被覆盖的次数,但通过懒标记更新整个子树)。
• minCoverLen:该区间内被覆盖次数等于minCover的底边长之和(用于计算未被覆盖的长度)。
• todo:懒标记,表示子树需要增加的覆盖次数(用于延迟更新)。
• 建树:初始化线段树,叶子节点的minCover为0(初始未被覆盖),minCoverLen为对应区间的长度(xs[i+1]-xs[i])。
5. 扫描线过程:
• 按y坐标从小到大处理事件(模拟从下往上扫描):
• 对于每个事件(y, lx, rx, delta),找到其对应的离散化区间[l, r](l为lx在xs中的索引,r为rx在xs中的索引减1)。
• 更新线段树:将区间[l, r]的覆盖次数增加delta(通过线段树的区间更新,包括懒标记处理)。
• 更新后,根节点维护整个x轴区间的信息:minCover表示整个区间被覆盖的最小次数(实际上根节点的minCover就是整个区间的最小覆盖次数,但这里我们关心是否被覆盖过?实际上,根节点的minCover为0表示有部分区间未被覆盖,否则全部被覆盖至少一次)。
• 计算当前被至少一个矩形覆盖的底边总长度sumLen:总长度(xs[-1]-xs[0])减去未被覆盖的长度(即根节点minCover为0时,minCoverLen就是未被覆盖的长度,否则为0)。
• 记录当前事件处理后的累计面积(totArea)和当前的sumLen(用于后续二分)。累计面积的计算:从上一次事件到当前事件的高度差(events[i+1].y - e.y)乘以当前的sumLen,得到这一段的面积,并累加到totArea。
6. 二分查找分割线:
• 总面积为totArea(所有正方形并集的面积),目标是找到y=Y使得下半部分面积为totArea/2。
• 在records中记录每个事件处理后的累计面积(当前事件之前的累计面积)和当前的sumLen(底边被覆盖的长度)。
• 二分查找最后一个累计面积小于totArea/2的事件索引i(即records[i].area
• 分割线Y的位置:从事件i对应的y坐标(events[i].y)开始,还需要上升的高度为(剩余面积差)除以(当前的底边被覆盖长度sumLen)。即:
Y = events[i].y + (totArea/2 - records[i].area) / records[i].sumLen
7. 输出结果:
计算得到的Y即为答案,要求绝对误差不超过1e-5。
时间复杂度和额外空间复杂度
• 时间复杂度:
离散化(排序去重):O(n log n),n为正方形数量(最多2n个坐标)。
事件排序:O(n log n)。
线段树建树:O(n)(实际节点数最多4N,N为离散化后区间数)。
线段树每次更新和查询:O(log n)(每次事件处理更新区间,最多2n次事件)。
二分查找:O(log n)。
总时间复杂度:O(n log n)。
• 额外空间复杂度:
离散化数组xs:O(n)。
事件数组events:O(n)。
线段树:O(n)(节点数最多4N,N为离散化后区间数,最多2n个点,区间数最多2n-1)。
records数组:O(n)。
总空间复杂度:O(n)。
注意:n为正方形数量(输入规模),但离散化后区间数最多为2n(去重后可能更少),因此线段树节点数为O(n)。所有操作都是基于n的多项式级别。
Go完整代码如下:
package main
import (
"fmt"
"math/bits"
"slices"
"sort"
)
// 线段树每个节点维护一段横坐标区间 [lx, rx]
type seg []struct {
l, r int
minCoverLen int// 区间内被矩形覆盖次数最少的底边长之和
minCover int// 区间内被矩形覆盖的最小次数
todo int// 子树内的所有节点的 minCover 需要增加的量,注意这可以是负数
}
// 根据左右儿子的信息,更新当前节点的信息
func (t seg) maintain(o int) {
lo, ro := &t[o
mn := min(lo.minCover, ro.minCover)
t[o].minCover = mn
t[o].minCoverLen = 0
if lo.minCover == mn { // 只统计等于 minCover 的底边长之和
t[o].minCoverLen = lo.minCoverLen
}
if ro.minCover == mn {
t[o].minCoverLen += ro.minCoverLen
}
}
// 仅更新节点信息,不下传懒标记 todo
func (t seg) do(o, v int) {
t[o].minCover += v
t[o].todo += v
}
// 下传懒标记 todo
func (t seg) spread(o int) {
v := t[o].todo
if v != 0 {
t.do(o
t.do(o
t[o].todo = 0
}
}
// 建树
func (t seg) build(xs []int, o, l, r int) {
t[o].l, t[o].r = l, r
t[o].todo = 0
if l == r {
t[o].minCover = 0
t[o].minCoverLen = xs[l+1] - xs[l]
return
}
m := (l + r) >> 1
t.build(xs, o
t.build(xs, o
t.maintain(o)
}
// 区间更新
func (t seg) update(o, l, r, v int) {
if l
t.do(o, v)
return
}
t.spread(o)
m := (t[o].l + t[o].r) >> 1
if l
t.update(o
}
if m
t.update(o
}
t.maintain(o)
}
// 代码逻辑同 850 题,增加一个 records 数组记录关键数据
func separateSquares(squares [][]int)float64 {
m := len(squares) * 2
xs := make([]int, 0, m)
type event struct{ y, lx, rx, delta int }
events := make([]event, 0, m)
for _, sq := range squares {
lx, y, l := sq[0], sq[1], sq[2]
rx := lx + l
xs = append(xs, lx, rx)
events = append(events, event{y, lx, rx, 1}, event{y + l, lx, rx, -1})
}
// 排序去重,方便离散化
slices.Sort(xs)
xs = slices.Compact(xs)
// 初始化线段树
n := len(xs) - 1// len(xs) 个横坐标有 len(xs)-1 个差值
t := make(seg, 2
t.build(xs, 1, 0, n-1)
// 模拟扫描线从下往上移动
slices.SortFunc(events, func(a, b event)int { return a.y - b.y })
type pair struct{ area, sumLen int }
records := make([]pair, m-1)
totArea := 0
for i, e := range events[:m-1] {
l := sort.SearchInts(xs, e.lx)
r := sort.SearchInts(xs, e.rx) - 1// 注意 r 对应着 xs[r] 与 xs[r+1]=e.rx 的差值
t.update(1, l, r, e.delta) // 更新被 [e.lx, e.rx] 覆盖的次数
sumLen := xs[len(xs)-1] - xs[0] // 总的底边长度
if t[1].minCover == 0 { // 需要去掉没被矩形覆盖的长度
sumLen -= t[1].minCoverLen
}
records[i] = pair{totArea, sumLen} // 记录关键数据
totArea += sumLen * (events[i+1].y - e.y) // 新增面积 = 被至少一个矩形覆盖的底边长之和 * 矩形高度
}
// 二分找最后一个
i := sort.Search(m-1, func(i int)bool { return records[i].area*2 >= totArea }) - 1
returnfloat64(events[i].y) + float64(totArea-records[i].area*2)/float64(records[i].sumLen*2)
}
func main {
squares := [][]int{{0,0,1},{2,2,1}}
result := separateSquares(squares)
fmt.Println(result)
}
Python完整代码如下:
# -*-coding:utf-8-*-
import bisect
class SegTree:
def __init__(self, xs):
self.n = len(xs) - 1
self.xs = xs
self.size = 1
while self.size
self.size *= 2
self.min_cover = [0] * (2 * self.size)
self.min_cover_len = [0] * (2 * self.size)
self.todo = [0] * (2 * self.size)
# 初始化叶子节点
for i in range(self.n):
self.min_cover_len[self.size + i] = xs[i+1] - xs[i]
for i in range(self.n, self.size):
self.min_cover_len[self.size + i] = 0
for i in range(self.size - 1, 0, -1):
self.maintain(i)
def maintain(self, o):
lo, ro = 2*o, 2*o+1
mn = min(self.min_cover[lo], self.min_cover[ro])
self.min_cover[o] = mn
self.min_cover_len[o] = 0
if self.min_cover[lo] == mn:
self.min_cover_len[o] += self.min_cover_len[lo]
if self.min_cover[ro] == mn:
self.min_cover_len[o] += self.min_cover_len[ro]
def do(self, o, v):
self.min_cover[o] += v
self.todo[o] += v
def spread(self, o):
if self.todo[o] != 0:
self.do(2*o, self.todo[o])
self.do(2*o+1, self.todo[o])
self.todo[o] = 0
def update(self, l, r, v, o=1, segL=0, segR=None):
if segR is None:
segR = self.size - 1
if l
self.do(o, v)
return
self.spread(o)
mid = (segL + segR) // 2
if l
self.update(l, r, v, 2*o, segL, mid)
if mid
self.update(l, r, v, 2*o+1, mid+1, segR)
self.maintain(o)
def separateSquares(squares):
m = len(squares) * 2
xs = []
events = []
for sq in squares:
lx, y, l = sq
rx = lx + l
xs.extend([lx, rx])
events.append((y, lx, rx, 1))
events.append((y + l, lx, rx, -1))
xs = sorted(set(xs))
events.sort(key=lambda x: x[0])
n = len(xs) - 1
seg_tree = SegTree(xs)
records = []
tot_area = 0
for i in range(len(events) - 1):
y, lx, rx, delta = events[i]
l = bisect.bisect_left(xs, lx)
r = bisect.bisect_left(xs, rx) - 1
seg_tree.update(l, r, delta)
total_len = xs[-1] - xs[0]
if seg_tree.min_cover[1] == 0:
total_len -= seg_tree.min_cover_len[1]
records.append((tot_area, total_len))
next_y = events[i+1][0]
tot_area += total_len * (next_y - y)
# 二分查找
target = tot_area / 2
left, right = 0, len(records)
while left
mid = (left + right) // 2
if records[mid][0] * 2 >= tot_area:
right = mid
else:
left = mid + 1
i = left - 1
if i
return float(events[0][0])
prev_area, total_len = records[i]
prev_y = events[i][0]
remaining_area = tot_area / 2 - prev_area
return prev_y + remaining_area / total_len
def main:
squares = [[0, 0, 1], [2, 2, 1]]
result = separateSquares(squares)
print(result)
if __name__ == "__main__":
main
·
我们相信Go语言和算法为普通开发者提供了困境的“面试利器”,并致力于分享全面的编程知识。在这里,您可以找到最新的Go语言教程、算法解析、提升面试竞争力的秘籍以及行业动态。
欢迎关注“福大规模架构师每日一题”实盘10倍杠杆,让 Go 语言和算法助力您的职业发展
港陆证券提示:文章来自网络,不代表本站观点。